Zeeman effect
原子的磁矩及在磁场中的能级分裂
- 电子的总磁矩:由自旋磁矩和轨道磁矩两部分矢量合成
- 由于
都绕着 旋进,又因为朗德g因子的不同,总磁矩也绕着 旋进。 - 有效磁矩:总磁矩
沿 方向的分量大小。 - 若存在外磁场,则原子磁矩在外磁场中存在取向势能
- 在外磁场较弱,不会破坏L-S耦合时原子总磁矩可用有效磁矩代替。
- 有效磁矩:总磁矩
从而,在弱磁场中取向势能为:
这表明原子能级在精细结构的基础上进一步按照
在多电子原子中,将单个电子的n,l,s,j改为多电子的N、L、S、J即可。
塞曼效应
把原子放入磁场中,其光谱线发生分裂,原来的一条谱线分裂成几条,且分裂后的谱线成分是偏振的,这种现象称为塞曼效应。
- 正常塞曼效应
现象:原有的谱线分裂成了等间隔的三条。 - 反常塞曼效应
现象:当磁场较弱时,塞满分裂的数目可以不是三条,也不一定等间隔。
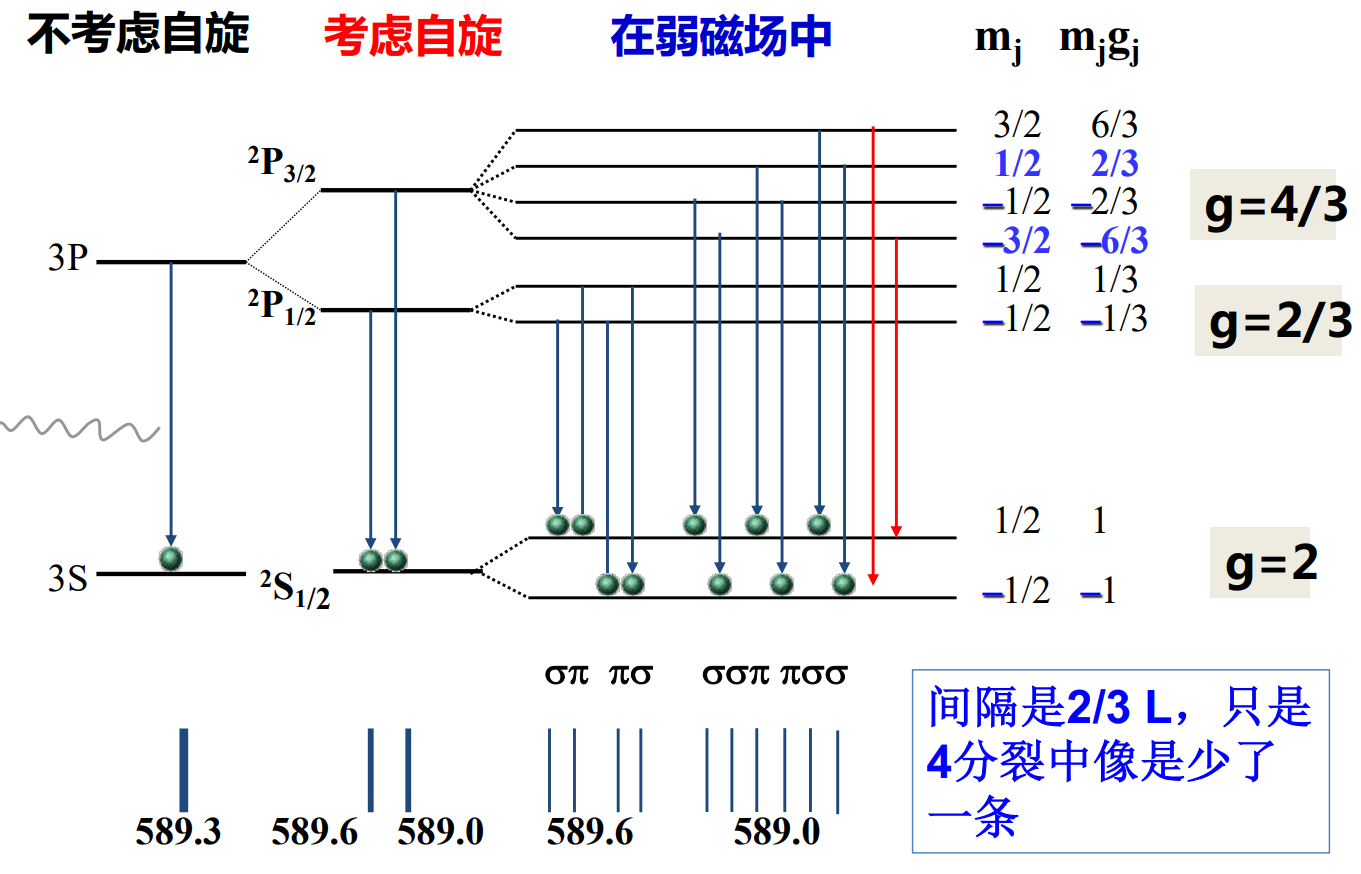
考察两个精细结构能级的跃迁:
- 无外磁场时:
之间的跃迁产生一条谱线: - 有外磁场时:原子磁矩的取向势能被引入体系(忽略相对论动能和势能修正项)
则两个能级各附加能量
代入洛伦兹单位
在没有自旋的情况下,经典原子的拉莫尔频率除以c。
格罗春图

帕邢-巴克效应
在强磁场下(B>Z^4T),l-s耦合被破坏,尽管L,S量子数仍有意义,但是总角动量J已经无意义了,此时l,s分别绕外磁场旋进。
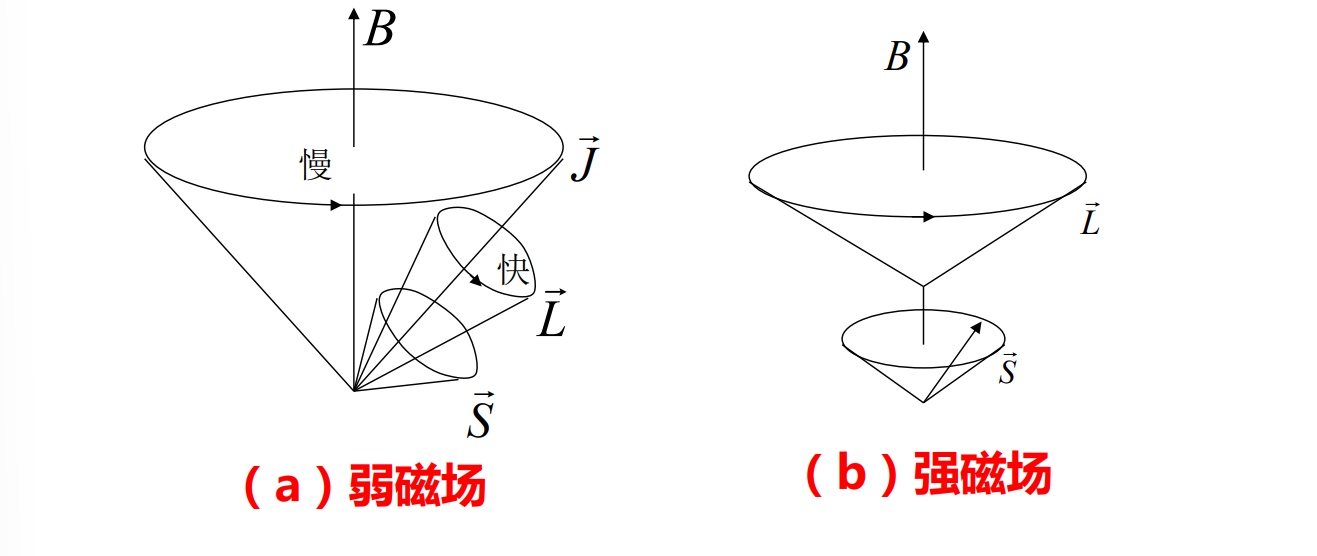
然而在1912年发现了原子谱线在强磁场中同样分裂的现象,此时谱线表现为正常(趋于)塞曼效应分裂。
此时磁矩与磁场相互作用产生的能级分裂为:
(选择定则:
| 正常塞曼效应 | 反常塞曼效应 | 帕邢-巴克效应 | |
|---|---|---|---|
| 自旋状态 | S=0 | S |
S |
| 磁场强弱 | 与磁场强弱无关 | 弱磁场 | 强磁场 |
| 谱线分裂条纹 | 3条 | 不一定 | 3条(但每条可能再分裂) |
| 朗德因子 | g=1 | g无定值 | 无朗德因子 |
| 自旋-轨道作用与外磁场作用比较 | 无自旋-轨道作用 | 自旋-轨道作用大于外磁场作用 | 自旋-轨道作用小于外磁场作用 |
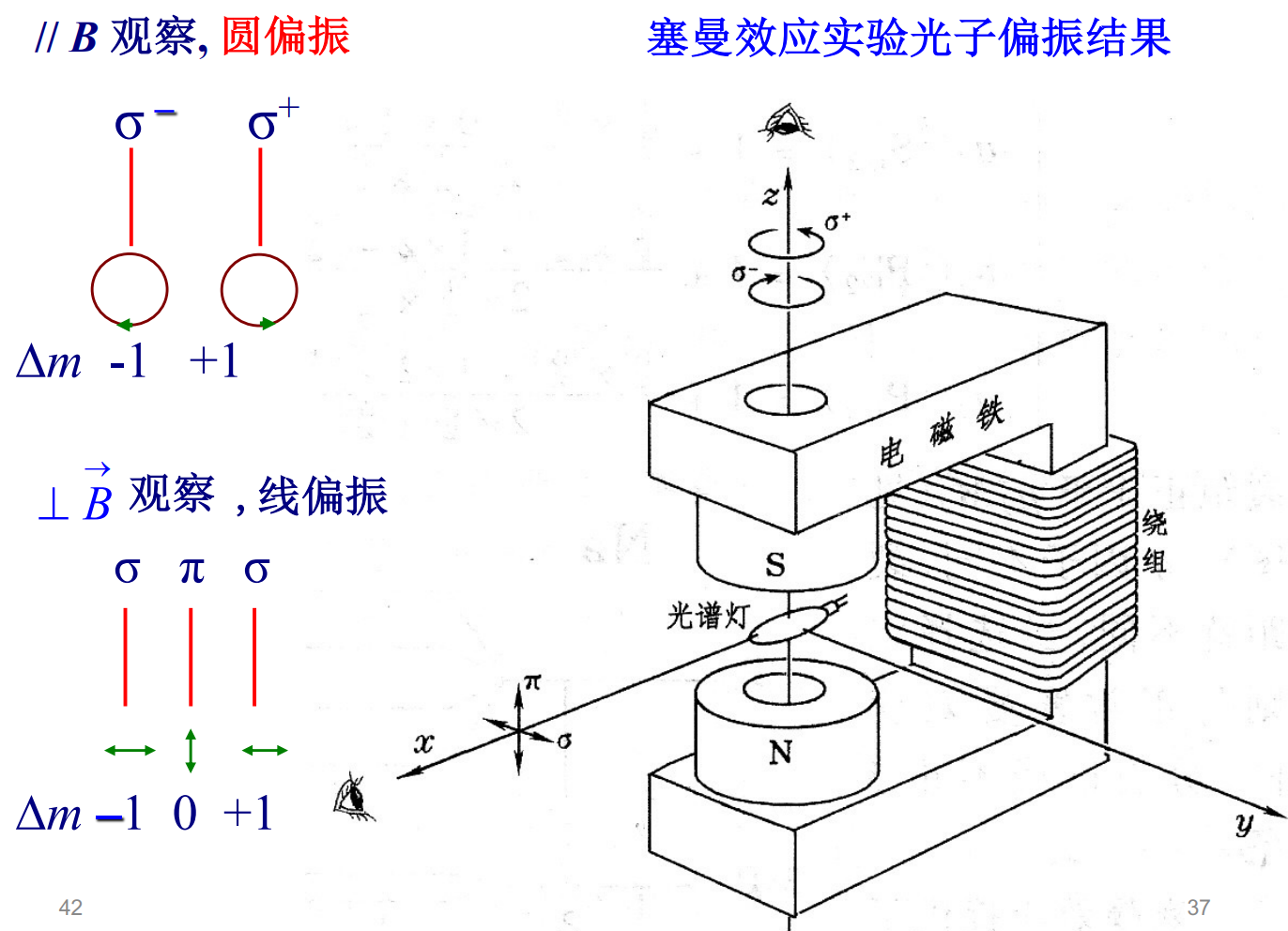
塞曼效应的偏振特性
在电磁学中,沿z方向传播的电磁波的电矢量一定在oxy平面:
其中A=B是圆偏振,
其中
光子的轨道角动量
光子的磁场B由角动量决定,光子的轨道角动量大小为
上图