Wave function and its significance

微观粒子由于波动性较强，其运动具有量子化的特点，不适合使用经典的牛顿定律去描述其运动规律，为了建立一个能描述微观粒子运动规律的方程， $S c h r \ddot{o} d i n g e r$ 方程应运而生。
因为自由粒子的能量E和动量p都是常量，所以由德布罗意关系可知，与自由电子联系的波的频率为 $μ$ 和波矢k（或波长 $λ$ ）都不变，即是一个单色平面波^[1]。描述一个频率为 $ν$ ,波长为 $λ$ ,沿单位矢量 $\vec{n}$ ,方向传播的平面波我们有：

Ψ = A c o s [2 π (\vec{r} \cdot \frac{\vec{n}}{λ} - ν t)] = A c o s [\vec{k} \cdot \vec{r} - ω t]

写成复数形式：

Ψ = A e^{[i (\vec{k} \cdot \vec{r} - ω t)]}

由德布罗意关系得到物质波的波动方程：

Ψ = A e^{[\frac{i}{ℏ} (\vec{p} \cdot \vec{r} - E t)]}

如果粒子处于随时间和位置变化的力场中运动时，其动量和能量就不再是常量（或不同时为常量），此时便不能用平面波描写，我们使用波函数 $Ψ (\vec{r}, t)$ 【 $Ψ (x, y, z; t)$ 】描写（通常是个复函数）。 $Ψ (\vec{r}, t)$ 不同于经典的波函数，其本身无直接的物理意义，有意义的是 $∣ Ψ ∣^{2}$ ，它表示在给定时间一个粒子出现在 $\vec{r}$ 处单位体积内的概率(由Born提出，是量子力学基本原理之一).即：

在t时刻、r点附近 $d τ = d x d y d z$ 体积内找到粒子的概率为： $d W (r, t) = C ∣ Ψ (r, t) ∣^{2} d τ$ ,C是比例系数
在t时刻r点附近，单位体积内找到粒子的概率是： $w (\vec{r}, t) = d W (\vec{r}, t) / d τ = C ∣ Ψ (r, t) ∣^{2}$ (概率密度)
在V内，t时刻找到粒子的概率为： $W (t) = \int_{V} d W (\vec{r}, t) = C \int_{V} ∣ Ψ (r, t) ∣^{2} d τ$

波函数的两种错误解释

波动性是大量粒子在空间疏密变化的一种分布，是一种疏密波——单电子衍射实验仍能出现衍射条纹，说明其错误。
粒子由波组成，电子是波包，把波包看成是电子的实际结构，是三维空间连续分布的物质波包，波包大小即电子大小，波包的群度即是电子的速度——自由粒子可由平面波描写，而平面波充满整个空间。然而实际上实验观测到的电子总是定域且完整的；且三维波包在传播的过程中扩散，如电子由波组成，着传播电子可能会越来越“胖”，甚至从不同的方向观察到的将是“电子的一部分”，而不是完整的。

#波函数的不定性
波函数表示的概率是相对的概率， $C Ψ (r, t)$ 和 $Ψ (r, t)$ 所描述的的状态的相对几率是相同的，因此波函数有一常数因子具有不确定性。为了确定常数因子，我们通常采取归一化处理。利用归一化条件我们有 $\int_{\infty} ∣ Ψ (r, t) ∣^{2} d τ$ ,波函数 $Ψ$ 称为归一化波函数^[2]。

#对波函数的要求
有限性，连续性，单值性

$∣ Ψ (r, t) ∣^{2}$ 是有限值，必须能够归一化
$∣ Ψ (r, t) ∣^{2}$ 必须是单值函数
$∣ Ψ (r, t) ∣^{2}$ 必须是连续函数，不能存在突变点

#波函数的种类

坐标波函数
1. 最常见的波函数形式
动量波函数
1. 将坐标波函数进行傅里叶变换获得： $Ψ (\vec{p}) = \int ψ (\vec{r}) e^{i \cdot \vec{p} \cdot \vec{r}} d^{3} \vec{r}$
角动量波函数
自旋波函数
···

叠加态原理

与经典的波相同，量子力学中的波也可以进行叠加；与经典的波不同，叠加态原理是态的叠加而非概率的直接相加，其相关原理成为叠加态原理

以电子的双缝干涉为例：

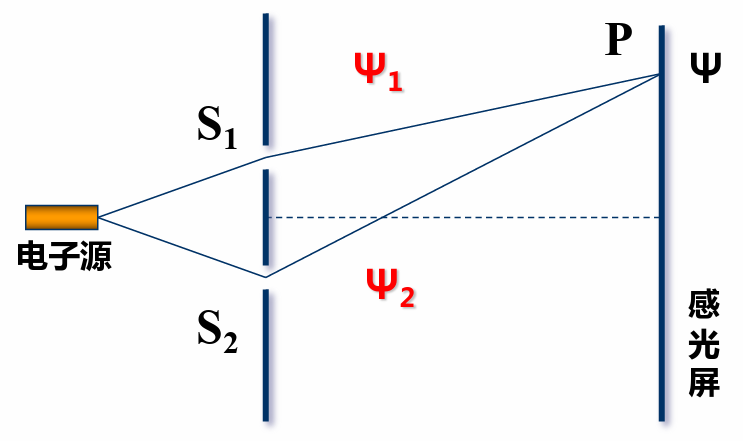
BE1A73EC108B5FDEEEEDC5F95FDC8D39.png|450
一个电子穿过双缝到达P点有两条路径，分别是穿过S1、S2到达P点；两条路径到达P的波函数分别为 $Ψ_{1}, Ψ_{2}$ ,则到达P的总波函数为：

∣ Ψ ∣^{2} =∣ C_{1} Ψ_{1} + C_{2} Ψ_{2} ∣^{2} =∣ C_{1} Ψ_{1} ∣^{2} + ∣ C_{2} Ψ_{2} ∣^{2} + (C_{1}^{*} Ψ_{1}^{*} C_{2} Ψ_{2} + C_{1} Ψ_{1} C_{2}^{*} Ψ_{2}^{*})

其中C1,C2为复常数；上式前两项分别为穿过对应的缝到达P点的概率，最后一项表示，两个概率波在P的干涉叠加^[3]。

#对电子双缝干涉的解释
在双缝后增加光源以确定电子位置时会导致叠加态的电子发生量子坍缩,干涉条纹随着光强增大逐渐消失。^[4]
双缝干涉实验中，是一个电子自身与自身的干涉叠加，而非两个电子的叠加，两个量子波的叠加并不形成一个新的状态。（电子与光子不同，光子静止质量为0，因此光子双缝干涉可以由经典波理论解释）。
宏观子弹射击实验未产生双缝干涉的原因在于其质量加大，波长过小，干涉效应过于细小——将干涉条纹进行横向压缩，因此我们只能观察到其平均效应。

海森堡不确定原理

经典体系中，任何粒子都具有其精确的位置、（角）动量和能量，然而对于波，其不可能具有完全确定的位置、动量等物理量。
维尔纳·海森堡，也是量子力学的创始人之一，“哥本哈根学派”代表性人物。1927年海森堡提出了不确定性关系：微观粒子的动量、能量和时间都具有不确定性^[5]。

#不确定原理表达式

粗略表达式： $Δ p \cdot Δ q \approx h$
改善表达式： $Δ p \cdot Δ q \geq h$
精确表达式： $Δ p \cdot Δ q \geq \frac{ℏ}{2}$ ; 不确定度被定义为标准偏差
分量形式： $σ_{x} \cdot σ_{p_{x}} \geq \frac{ℏ}{2}$ ··· y、z方向同理

物理意义

当粒子的动量完全确定时（ $Δ_{P_{x}} ⟶ 0$ ），其位置完全不确定（ $Δ x ⟶ \infty$ ）,反之亦然。这说明我们从客观事实上就无法同时得到粒子的精确位置与动量，而非测量技术问题。不确定关系给出了经典理论的适用界限，同时我们也无法使用轨道概念来描述微观粒子的运动。

例：对于单缝衍射，大部分电子打到主极大位置是确定的，缝的宽度是位置不确定的d，偏移主极大的角度θ是不确定的，继而动量的偏移量 $Δ \vec{p} = \vec{p} s i n θ$ ，因此有 $Δ p Δ q = h$ .

微粒能量与时间的不确定关系

能量与时间的不确定性的关系
一个体系处于某个状态，如果有一段时间的 $Δ t$ 的时间不确定性，那么他的能量也有一个范围 $Δ E$ 的不确定性，二者的乘积有以下关系：

Δ E \cdot Δ t \geq \frac{ℏ}{2}

公式的推导
微观粒子的能量(Relativistic dispersion relation)为：

E = m c^{2} = \sqrt{p^{2} c^{2} + m_{0}^{2} c^{4}}

对上式取微分

d E = \frac{1}{2} \frac{1}{\sqrt{p^{2} c^{2} + m_{0}^{2} c^{4}}} \cdot 2 c^{2} p d p = \frac{c^{2} p d p}{E} = \frac{p d p}{m} = v d p

同乘 $Δ t$ 有： $Δ E \cdot Δ t = Δ p \cdot v Δ t = Δ p \cdot Δ q \geq \frac{ℏ}{2}$

物理意义
- 在原子光谱中, 光谱的宽度（能量的范围 $Γ = Δ E$ 是吸收峰的半高宽又称粒子的宽度）和激发态电子的寿命（ $τ = Δ t$ ）具有不确定关系，因此我们有：^[6]

Γ τ = ℏ \geq \frac{ℏ}{2}

回答薛定谔的诘难：
1. 跃迁过程中电子能量完全不确定
2. 跃迁过程中电子没有中间态停留，跃迁不需要时间

微粒角动量与角位移的不确定性关系

角动量L与角位移 $θ$ 之间有不确定性关系

Δ L \cdot Δ θ \geq \frac{ℏ}{2}

公式的推导

d L = m d v \cdot r = d p r

Δ p \cdot Δ q = Δ p \cdot v Δ t = Δ p \cdot ω r Δ t = Δ p \cdot Δ θ r = Δ L \cdot Δ θ \geq \frac{ℏ}{2}

不确定关系的意义

不确定关系说明用经典物理学量——动量、坐标来描写微观粒子行为时将会受到一定的限制，因为微观粒子不可能同时具有确定的动量及位置坐标，没有确定的轨道。
不确定关系可以用来判别对于实物粒子其行为究竟应该用经典力学来描写还是用量子力学来描写。不确定量是微不足道时，实物粒子的行为仍可用经典力学处理。
不确定关系是波粒二象性导致的定量结果

不确定关系联系的是数学上的两个共轭变量，一般是傅立叶变换的关系，与其对易关系有关。

Chatgpt的解释

这句话指的是在数学和物理学中常见的一种关系。在傅立叶变换中，有时候我们处理的是一对共轭变量，例如时间域和频率域之间的关系。这种关系中的一个变量的精确值的确定性会影响另一个变量的不确定性。

以时间域和频率域为例，傅立叶变换将信号从时间域转换到频率域。在时间域中，信号的精确值是已知的，但在频率域中，对应的频率成分的确切位置可能会受到时间域信号的特定形状和频谱内容的影响而产生一定的不确定性。

这种关系也可以用于解释不确定性原理中的一些概念。例如，根据海森堡不确定性原理，在量子力学中，粒子的位置和动量不能同时被准确确定。这就类似于傅立叶变换中的时间域和频率域之间的关系，其中一个变量的确定性会影响到另一个变量的不确定性，从而体现了不确定关系。

不确定关系的应用：

光谱线的自然宽度
估算宏观物体的不确定性
证明原子中电子运动不存在“轨道”
证明原子核中不可能禁锢电子。

下一节：薛定谔方程

单色平面电磁波是指仅以单一频率随时间变化的平面电磁波。即：电磁波的的电分量表达式 $\vec{E} = \vec{E_{0}} e^{j (\vec{k} \cdot \vec{r} - ω t)}$ ,中仅有一个常数 $ω$ 决定其频率。 ↩︎
不是任何波函数都能归一化，如平面波函数，其描述的平面波在空间中无限延申无法归一化。同时归一化波函数仍具有一个模为一的复因子exp{iα},α为实数，其仍不确定性，exp{iα}ψ也是归一化波函数。 ↩︎
干涉项可正可负，也就是说在极端情况下概率可以为零，这取决于粒子的状态。 ↩︎
个人认为这和信息守恒相关，射出的电子的状态本是位置的，其信息要在其打到屏幕后才出现，但若在其路径上拦截其信息，必定会对其造成影响。亦即我们无法对运动中的电子不进行任何外部干涉而获得其信息。 ↩︎
自然界的客观规律而不是测量技术和主观能力的问题,即：粒子在客观上不能同时具有确定的坐标位置及相应的动量。因而“不能同时精确地测量它们” ↩︎
推导过程孩子还不会Q $Λ$ Q ↩︎