Transition rules and the principle of homogeneity

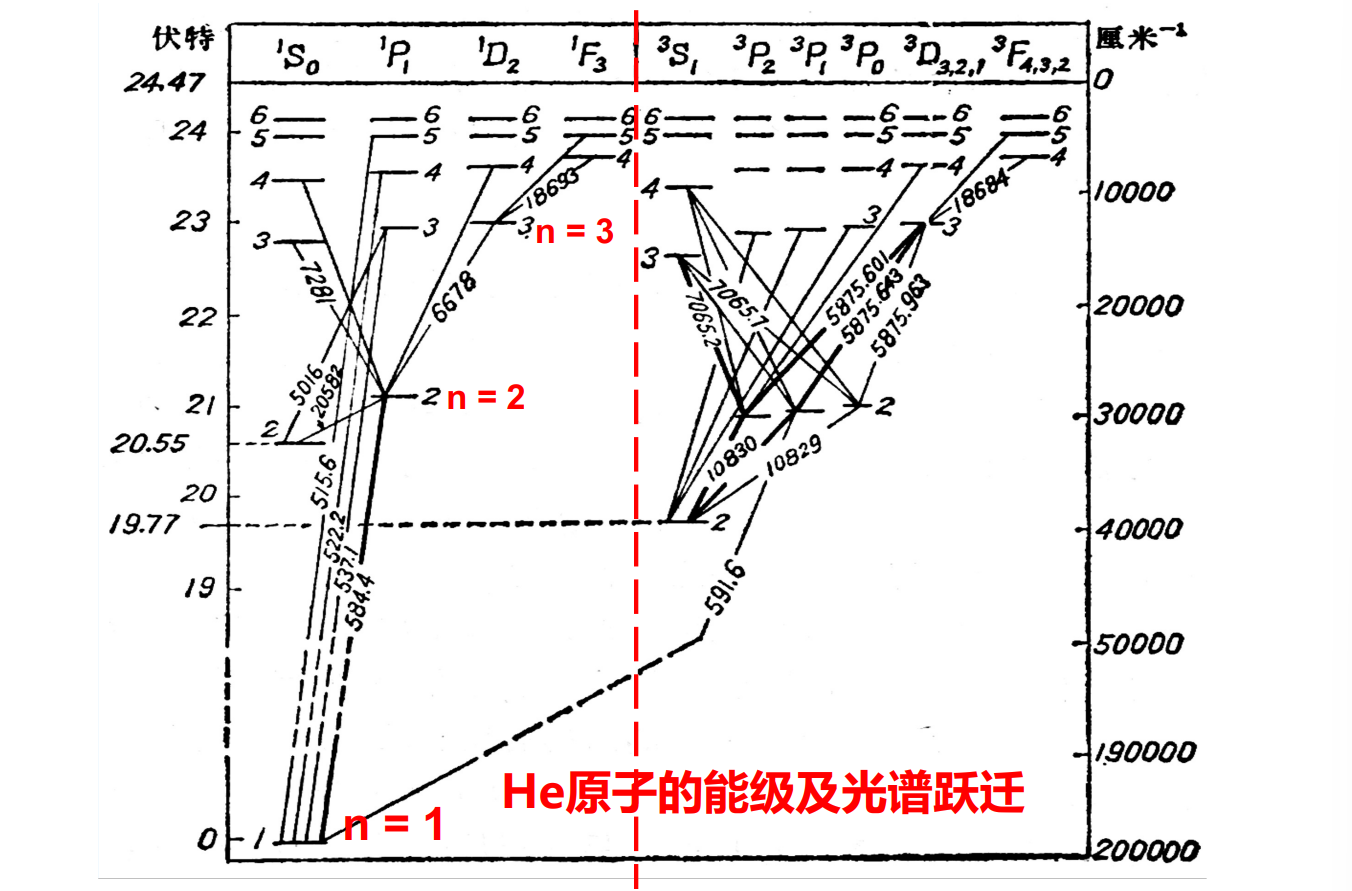
Pasted image 20240611041909.png
观察He原子光谱，我们不难发现一些细节之处：

三重态的能量总是低于单重态
基态的三重态和一些其他态缺失

选择定则

实际上电子在两个状态间的跃迁并非是任意的，能够发生跃迁的两个状态间必须满足一定的关系^[1]，这种关系称为跃迁的选择定则。
跃迁定则根据电子的耦合类型不同而不同：

L-S耦合
1. $Δ S = 0$
2. $Δ L = 0, \pm 1$
3. $Δ J = 0, \pm 1$
J-J耦合
1. $Δ j = 0, \pm 1$
2. $Δ J = 0, \pm 1$
  而He原子正是因为不满足第一个准则从而存在三重态和单重态间的跃迁禁阻。

泡利不相容原理

量子表述：在一个原子中，不可能有两个或两个以上的电子具有完全相同的四个量子数 ( $n ， l ， m_{l}, m_{s}$ )
普遍表述：在由费米子^[2]组成的系统中，不可能有两个或两个以上的粒子具有完全相同的状态。

这就解释了为什么会出现能级空缺的现象。
同时由于泡利不相容原理的存在，原子的内层能容纳的电子数目有限，需要不断地将电子填入新轨道，因此随着核电荷数升高，原子的大小的改变却并不明显，对金属加热不会逸出电子也是同样的道理：将内层电子激发逸出所需要的能量远高于晶格能。

同科电子的偶数定则

同科电子指n，l相同的电子；根据泡利原理，两个电子组成的系统其原子Ｌ＋Ｓ必为偶数。即：Ｌ＋Ｓ为偶数的原⼦态是符合泡利原理的，Ｌ＋Ｓ为奇数的原⼦态是违反泡利原理的（是空缺的）。
对于两个同科^[3]电子：

{\begin{array}{r} 自 旋 平 行 ， 即 总 自 旋 S = 1 ， m_{s} 相 同 \Rightarrow m_{l} 必 不 相 同 \Rightarrow 空 间 取 向 不 同 \Rightarrow 电 势 能 低 (稳 定) \\ 自 旋 反 平 行 ， 即 总 自 旋 S = 0 ， m_{s} 不 同 \Rightarrow m_{l} 可 以 相 同 \Rightarrow 空 间 取 向 相 同 \Rightarrow 电 势 能 高 (不 稳 定) \end{array}

这就解释了三重态原子能量更低的原因。（数学解释）

全同性原理

全同粒子：内禀性质完全相同的微观粒子。

内禀性质

粒子的内禀性质包括：静质量、电荷、自旋、寿命、味、色等

全同粒⼦所组成的体系中，两全同粒⼦相互调换不引起体系物理状态的改变——运动规律对全同粒子不可分辨。

吉布斯佯谬

吉布斯在其关于统计⼒学基础的⼯作中给出的⼀个简单⽽深刻的看法。假如我们有⼀个分隔成两个相等⼤⼩空间A和B的盒⼦，⼆者都充满着温度相同、密度相同的氢⽓。假设有⼀个开关将这两个空间隔开，如果打开开关让⽓体达到平衡。原来禁闭在A（或B）中的分⼦可能会出现在A+B中的任何地⽅。这样，因为分⼦分布似乎存在更多不同的可能性，量度可能微观状态数的⽓体的熵看来将会增加。但是基于经验，⼈们可能会有相反的直觉，即处于平衡态的⽓体的性质完全由其体积、温度和密度来表征。** 如果这个经验是正确的，那么打开开关的动作没有使⽓体的状态产⽣任何变化，当然它也就没产⽣任何熵。**
然而，如果我们能跟踪每一个分子，我们肯定会有额外的熵，即所谓的混合熵。确实，当不同种类的气体比如说氢和氦混合时，熵产生了。因为（表观上）类似气体的混合熵从没有被观测到，所以甚至在原则上也没有任何办法表明它们的分子分开了。因此我们不可能作这样一种严格的陈述：“分子1在A中，分子2在A中，……，分子n在A中” ，而只能给出一种弱得多的说法：“有n个分子在A中” 。

空间波函数

由于不确定性原理，我们所能探测的粒子轨迹所能达到的精度存在一个限度，因此我们在求解一个量子过程的时候必须把来自于所有可能出现方式的贡献求和。例如，两个全同粒子分别由1，2两个位置出发，随后进行相互作用后分别到达3，4位置。这里就有如图所示的两种可能：
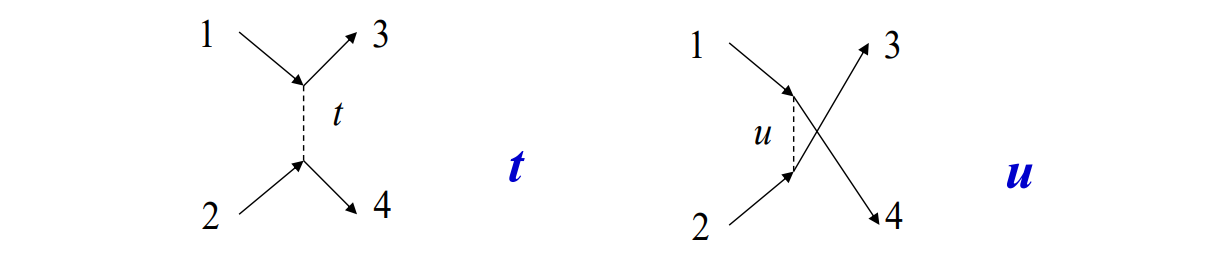
Pasted image 20240611231243.png

$1 \to 3; 2 \to 4$
$1 \to 4; 2 \to 3$
因此我们在求解薛定谔方程时，需要将两种情况到考虑到。然而，数学上的自洽严格性限制了我们的自由。
我们必须要求当我们对中间时间的态求和时，几率振幅相乘的法则与总几率幅的法则自洽。因为交换两次的最终结果与根本没有交换是相同的，所以我们必须这样来指定因子，即直接×直接=交换×交换，而唯一的自洽可能性是：直接/交换=±1。这分别对应于玻色子（+），和费米子（-）。符号的这种选择决定了直接贡献和交换贡献之间的干涉项对几率振幅模的平方，亦即总过程的几率的贡献。

玻色子与费米子

定义：
玻色子：是波函数具有交换对称性的粒子，即：对于两个坐标分别为 $r_{1}, r_{2}$ 的粒子，其波函数具有如下性质 $ψ (r_{1}, r_{2}) = ψ (r_{2}, r_{1})$
费米子：是波函数具有交换反对称性的粒子，即：对于两个坐标分别为 $r_{1}, r_{2}$ 的粒子，其波函数具有如下性质 $ψ (r_{1}, r_{2}) = - ψ (r_{2}, r_{1})$
性质：在量子场论中，通过自旋统计定理我们可以得到：玻色子的自旋量子数为整数、费米子的自旋量子数为半整数。
意义：
Bose-Einstein Condensation：多个玻色子可以占据同一个量子态，使得在低温时会出现大量玻色子聚集到同一个最低能量的状态，形成一种新物质状态。这种现象在超流体和超导体中有重要应用。
Pauli Exclusion Principle：对于费米子，泡利不相容原理指出，两个费米子不能占据相同的量子态。这是因为如果两个费米子占据同一量子态，波函数在交换这两个粒子时将变为零，意味着这种状态不存在。

上面例子的解答：
Pasted image 20240612004545.png

自旋波函数

$σ_{+} (σ_{-})$ 表示自旋向上（向下）的自旋态，两电子体系的自旋波函数就有四种可能：

σ_{+} (1) σ_{+} (2) σ_{-} (1) σ_{-} (2) σ_{+} (1) σ_{-} (2) σ_{-} (1) σ_{+} (2)

其中后两种不满足任何交换对称性，但是由于全同性原理要求费米子波函数的交换反对称，因此和前面坐标波函数一样我们需要对这几个波函数进行线性组合，使其全部具有交换对称性( $↑↑ o r ↓↓$ 构成三重态)。

X_{s} = {\begin{array}{r} σ_{+} (1) σ_{+} (2) M_{S} = 1 \\ \frac{1}{\sqrt{2}} [σ_{+} (1) σ_{-} (2) + σ_{-} (1) σ_{+} (2)] M_{S} = 0 \\ σ_{-} (1) σ_{-} (2) M_{S} = - 1 \end{array}

若要反对称的自旋波函数（ $↑↓$ ,构成单态），总自旋为零，可以写成如下形式：

\frac{1}{\sqrt{2}} [σ_{+} (1) σ_{-} (2) - σ_{-} (1) σ_{+} (2)]

其中 $\frac{1}{\sqrt{2}}$ 称为Clebsch-Gordan 系数，可以从群论的运算规则得到。

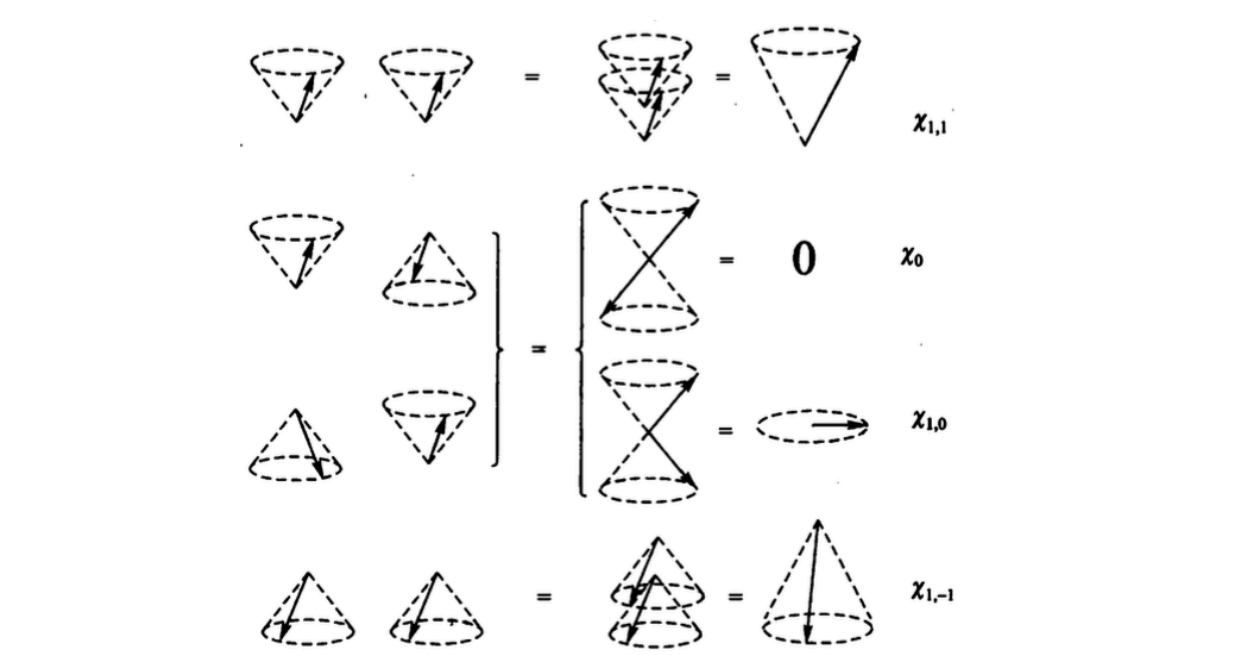
Pasted image 20240612014310.png
图中1.3.4个分别代表交换对称的三种自旋耦合方式，第2个位自旋反对称的耦合方式。

总波函数

电子的总波函数由空间波函数u和自旋波函数 $χ$ 组成，即 $Ψ = u χ$ 也应当遵守全同性原理满足交换反对称性。空间波函数正比于球谐函数 $Y_{L M}$ ,而球谐函数的交换对称性的本征值满足 $(- 1)^{L}$ ^[4],L为偶数时交换对称本征值为1，此时空间波函数是对称的；当L为奇数时，本征值为-1，此时空间波函数是反对称的。

具体的，以一个三重态的He原子为例，其中一个电子是基态，用 $ϕ_{0}$ 表示他的空间波函数，另一个电子处于主量子数为n，角动量量子数为l的态 $ϕ_{n l}$ 。结合上面提到的自旋波函数，我们可以写出它的总波函数^[5]：

Ψ = [ϕ_{0} (r_{1}) ϕ_{n l} (r_{2}) - ϕ_{0} (r_{2}) ϕ_{n l} (r_{1})] (\begin{array}{r} χ_{1, 1} \\ χ_{1, 0} \\ χ_{1, - 1} \end{array})

这里是空间部分反对称，自旋部分对称的波函数。当 $r_{1} = r_{2}$ 时，波函数为零，说明两个电子不可能离得很近。
若是与上述情况反过来（变为单态），则有如下波函数：

Ψ^{*} = [ϕ_{0} (r_{1}) ϕ_{n l} (r_{2}) + ϕ_{0} (r_{2}) ϕ_{n l} (r_{1})] χ_{0, 0}

此时波函数表明两个电子可以靠的很近，电荷的斥力会使得系统能量升高，因此这也印证了前面所说的单重态能量高于三重态的解释。

综上所述：两个电子的自旋交换对称性取决于 $(- 1)^{S + 1}$ ，两个电子的空间总波函数交换对称性取决于 $(- 1)^{L}$ ，总的波函数交换对称性为 $(- 1)^{S + L + 1}$ ，因为费米子需要满足交换反对称的性质，所以L+S为必须为偶数。对于全同的玻色子，其L+S也应该为偶数（这是因为玻色子及其反粒子内禀宇称之积为+1）

至此，量子力学的五个基本原理都已经展开讲述。

实际上再能够跃迁的能级中跃迁也非完全随机，而是有一定的概率分布。然而量子力学并不能对其做出解释，需要用到量子场论。 ↩︎
自旋量子数为 $\frac{1}{2}$ 的奇数倍的微观粒子，如电子，质子，中子。光子自旋量子数为1，是玻色子。 ↩︎
这里是同科电子，所以后面不会出现S, $m_{l}$ 不同的情况。 ↩︎
与宇称相关 ↩︎
总波函数也要满足交换反对称，因此两个函数不可能同时是反对称或对称的。 ↩︎