The Schrödinger equation under Coulomb force field
假设目标粒子除了库仑力不受其他任何作用,库仑力场下的薛定谔方程表现为:
因为势能作为有心力场是球对称的(与,无关),因此我们选用球坐标系来描述薛定谔方程:
其中中括号的后两项乘上就是轨道角动量平方算符.
定义角动量升降算符:和;他们分别可以将本征函数的特征值增加/减少.
由对易关系:;
因为
将总波函数分为径向和角向两个部分:
对上式两边同时除以得:
等式两边分别只含r和,要使等式成立,等式两侧只能等于常数;分别得到径向方程和角向方程:
角向方程
将角向方程继续分解,代入:
对上式两边同时乘以得:
的通解为:
由于球坐标系中只能取,又因为波函数的周期性和单值性:因此我们有:
而的解恰好是在某一方向上(通常取z方向)角动量算符的本征值方程的解,是磁量子数m乘以约化普朗克常数.
的解为勒让德多项式:
- 关联勒让德函数:
- 勒让德多项式:
则角向方程的解为:
归一化常数又被称为球谐函数,是角动量算符的本征函数,其中,,,,为角量子数为磁量子数.习惯上根据角量子数的不同我们对波函数的状态进行分类为:s,p,d,f...
径向方程
E>0 时,E 取任何值,方程都有满足波函数条件的解,即能量具有连续谱,电子可以运动到无限远处; E<0时,能量E取分立值,电子处于束缚态。下面我们重点研究 E<0 的情况。
求解过程一堆,复杂的一······ 懒得敲了,下面直接上吕才典老师PPT上的截图(有机会再补吧):
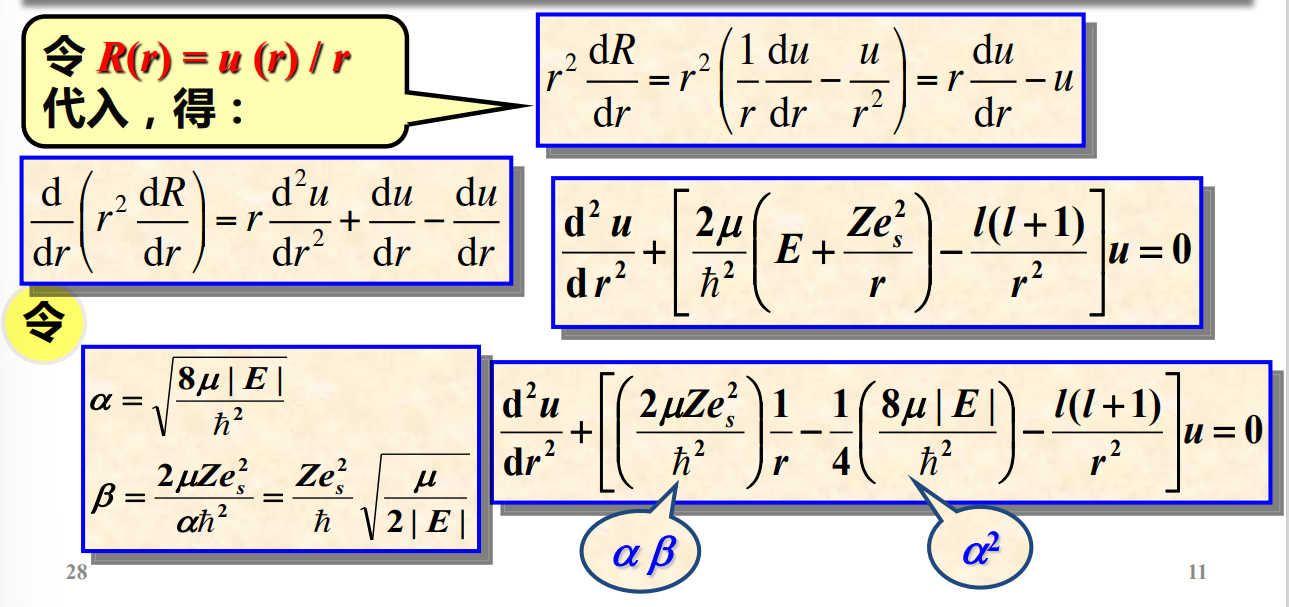
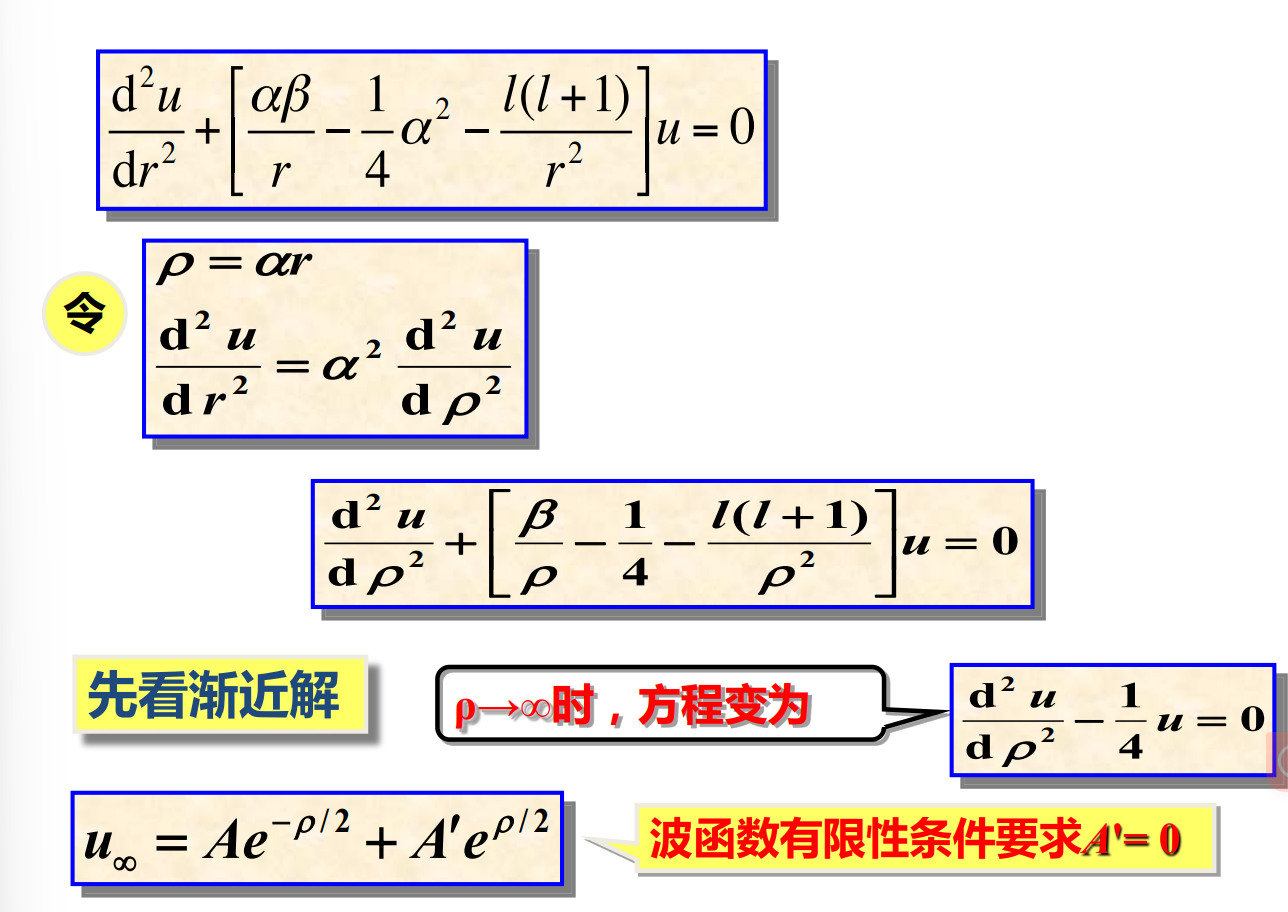
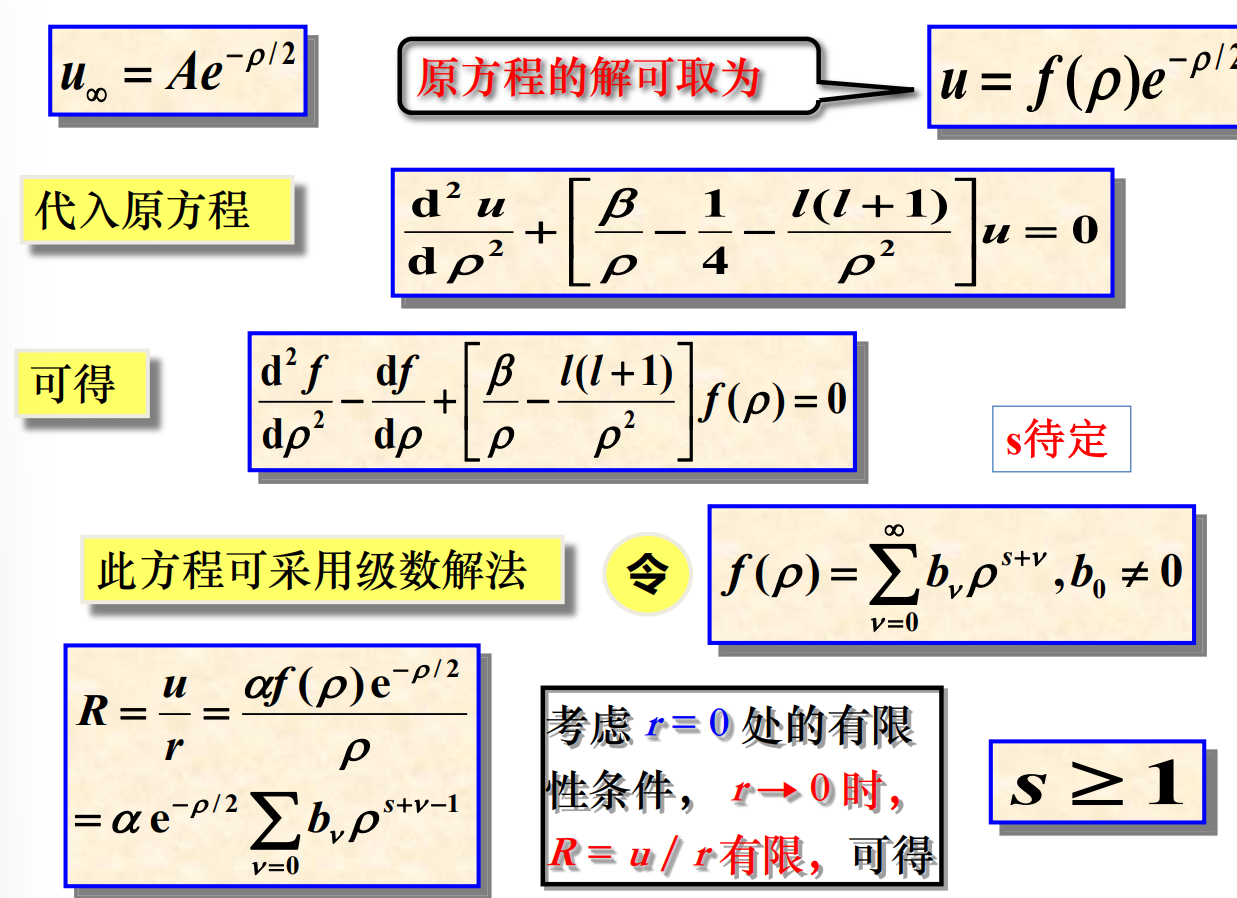


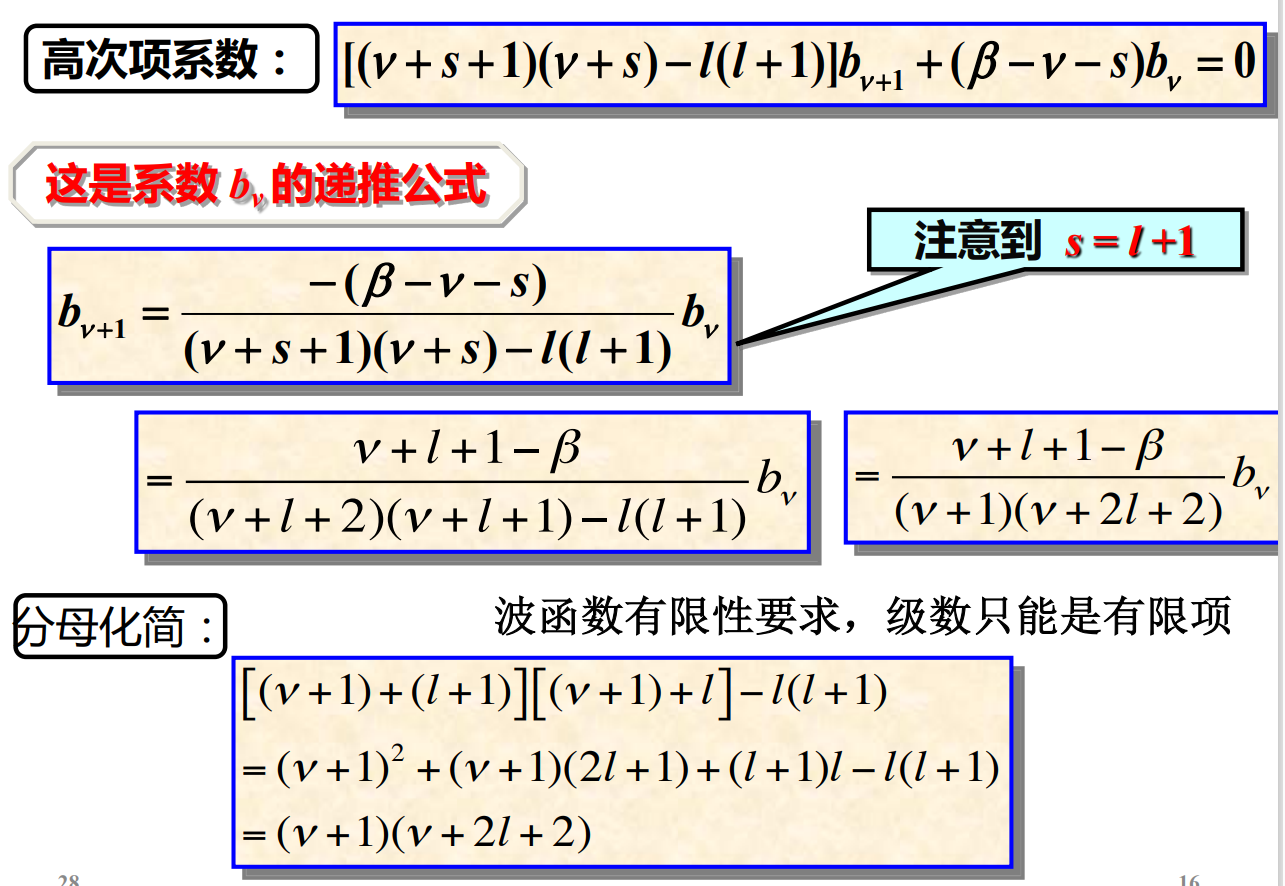
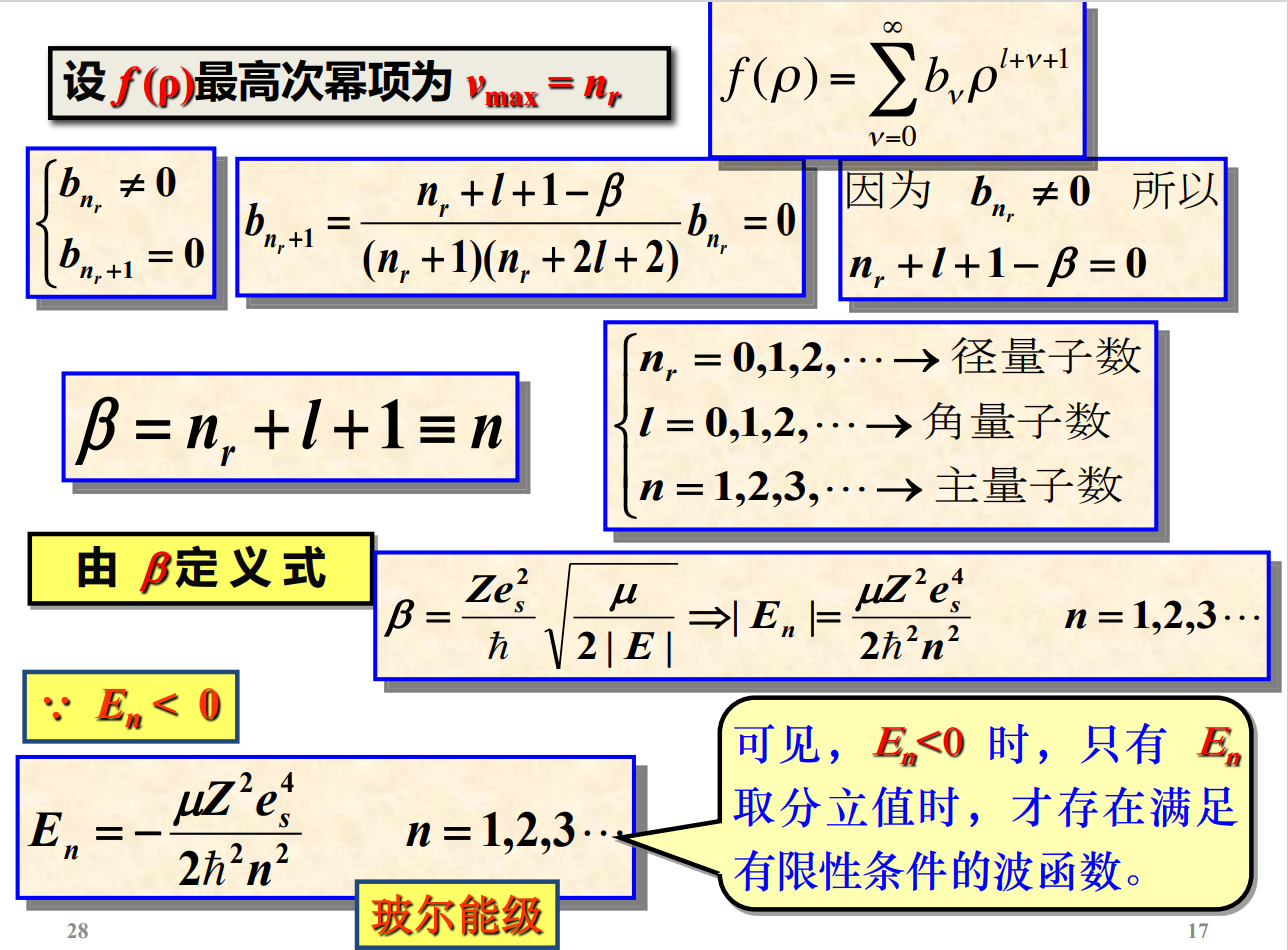


小结
设波函数的形式为:,分别与,有关。
由于波函数必须满足标准化条件,所以,这三个物理量都自然得出量子化的结果.
主量子数角量子数磁量子数能级简并
能量只与主量子数有关,态函数与n,l,m有关,能级存在简并。n确定后,,的最大值为n-1.l确定后,,一共个值。对于能级其简并度为:.几乎每个能级都有多个简并态,特别的,n=1时只有一个状态,是非简并的,这个状态就是我们常说的基态。
简并度与立场对称性
由上面求解过程,可以知道,由于库仑场是球对称的,所以径向方程与m 无关,而与 l 有关。因此对于一般的有心力场,我们考虑简并度只考虑对m的简并,即一个n的简并度为(2l+1),在库仑势场中,能量与l有关,因此出现了对l的简并,这种简并称为附加简并,是具有更高对称性的体现。
宇称
宇称是描述粒子在空间反演下变换性质的相乘性量子数,引记为P。定义一个线性变换:
即,空间坐标发生反号,但是时间不变的变换。虽然对于⼀个特定的点来说,变换的效果等价于某种转动。 但对于⼀个物理状态来说,它不完全等效于某种转动。在微观物理中,变换直接和宇称守恒相联系。
例:,即具有宇称
对于:
P只有两个值+1和-1。如果描述某一粒子的波函数在空间反演变换(r→-r)下改变符号,该粒子具有奇宇称(P=-1),如果波函数在空间反演下保持不变,该粒子具有偶宇称(P=+1);n个粒子组成的系统的宇称等于这n个粒子宇称之积再乘以这n个粒子之间的n-1个轨道宇称之积;轨道角动量量子数为1时,其轨道宇称为(-1)。玻色子及其反粒子内禀宇称之积为+1;费米子及其反粒子内禀宇称之积为-1。在强相互作用和电磁作用过程中宇称守恒,在弱作用过程中宇称不守恒。
宇称量子数是纯粹的量子特性,在粒子物理里有非常重要的应用,在这里它反映的是电磁相互作用里的空间反演对称性。在原子物理里,我们均讨论电磁相互作用,因此这个量子数是守恒的(即初态末态相同)。
粒子内部波函数存在的宇称,与其内部运动性质有关,在量子场论中得到理论的描述。
下一节:氢原子的量子模型
!200注释4图









