Fine structure correction of hydrogen atom energy level

氢原子的精细结构修正

在之前，我们已经提到过索末菲为了解释精细结构引入了相对论修正和椭圆轨道修正轨道。但是我们知道，实际上根据波函数的假设，原子内的电子并非以绕核旋转的形式进行运动。因此我们需要从新的角度进行修正——自旋轨道相互作用和自旋轨道耦合。
……
经过一系列的推导后我们得到：

仅考虑电子与原子核的库伦相互作用：能量仅与n有关。

E_{n} = - \frac{Z^{2} m_{e} c^{2} α^{2}}{2 n^{2}}

若进一步考虑相对论动能修正:可以看出能量不仅与n有关还与l有关，能级对轨道的简并解除，能级下移。

Δ E_{m} = - \frac{α^{2} Z^{2}}{n^{2}} E_{n} (\frac{3}{4} - \frac{n}{l + \frac{1}{2}})

进一步考虑自旋—轨道相互作用：自旋的大小也对能级产生影响

{\begin{array}{r} Δ E_{l, s} = 0 (l = 0) \\ Δ E_{l, s} = - \frac{α^{2} Z^{2}}{n^{2}} E_{n} n \frac{j (j + 1) - s (s + 1) - l (l + 1)}{2 l (l + \frac{1}{2}) (l + 1)} (l \neq 0) \end{array}

对于同一轨道角动量自旋量子数不同的情况下产生能级裂分： $J = \frac{1}{2}$ 的能级差为：

Δ E_{l s}^{'} = - \frac{α^{2} Z^{2}}{n^{2}} E_{n} n \frac{1}{l (l + 1)}

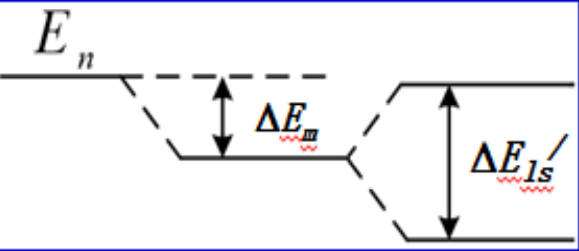
Pasted image 20240521225320.png|300 $Δ E_{m}$ 为相对论动能修正， $Δ E_{l s}$ 为自旋轨道相互作用修正。
4. 再引入相对论势能修正： $E_{V}$ ,因为其大于零，因此能级再次上移。

Δ E_{V} = {\begin{array}{r} - \frac{α^{2} Z^{2}}{n} E_{n} (l = 0) \\ 0 (l \neq 0) \end{array}

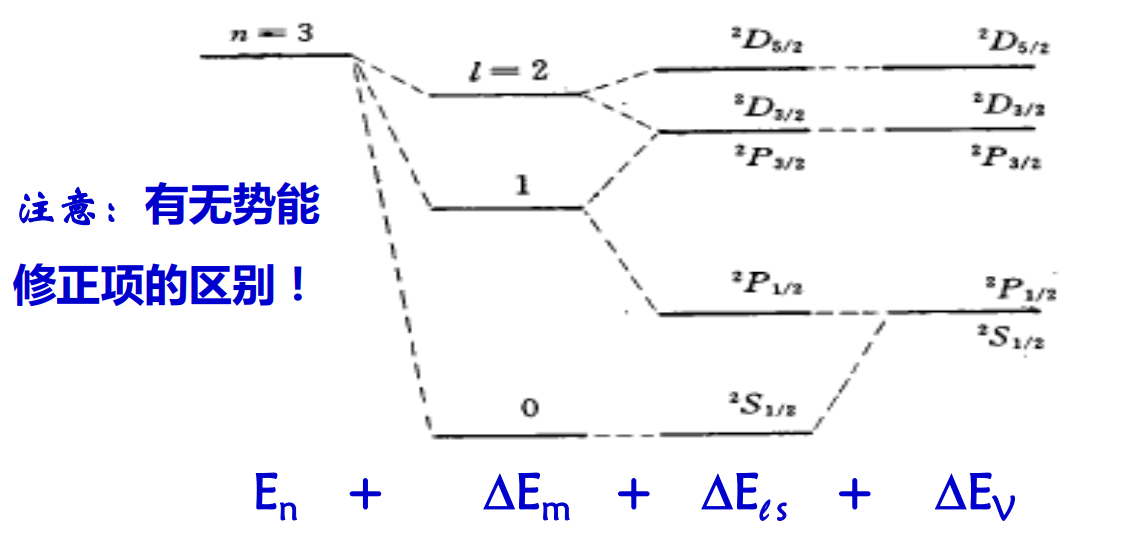
Pasted image 20240521230301.png

E = - \frac{h c R}{n^{2}} - \frac{h c R α^{2}}{n^{4}} (\frac{n}{j + \frac{1}{2}} - \frac{3}{4})

原子态符号表示

多重态结构的原子态符号表示：

n^{2 s + 1} L_{j}

其中2s+1是自旋多重度，表示原子态的重数，L代表轨道角动量的取向：S、P、D、F……
基态原子的自旋是L=0，S=max{s}时的原子态

跃迁的选择定则

由于光子的自旋是一，根据总角动量守恒 $Δ j = 0, \pm 1$ ,即跃迁前后总角动量的改变不能大于一。（多光子跃迁除外）
由于光子的宇称为负，根据电磁相互作用宇称守恒 $Δ l = \pm 1$ ，即放出单个光子后宇称改变。

兰姆位移与反常磁矩

在考虑了相对论动能修正效应 ΔEm，自旋轨道耦合修正效应：ΔEls，相对论势能修正效应：ΔEV后，氢原子能级 n=3 的精细结构图如上。注意能级有简并情况。例如根据最终能级修正结果有 $2^{2} S_{1 / 2}$ 与 $2^{2} P_{1 / 2}$ 能量相同， $3^{2} P_{3 / 2}, 3^{2} D_{3 / 2}$ 能量相同， $4^{2} D_{5 / 2}, 4^{2} F_{5 / 2}$ 能量相同。这些简并结果也可以从量子力学相对论狄拉克方程中严格导出，因此在相当长的一段时间内，这些简并被认为是严格的，直到更高精度的能级测量实验出现
实际上，与理论值相比，实验上在巴尔末系 $3^{2} P_{3 / 2} ⟶ 2^{2} S_{1 / 2}$ 相比于 $3^{2} D_{3 / 2} ⟶ 2^{2} P_{1 / 2}$ 的波数差了0.011 $c m^{- 1}$ ，帕斯特耐克指出如果 $2^{2} S_{1 / 2}$ 比 $2^{2} P_{1 / 2}$ 高出0.03 $c m^{- 1}$ 就可以说明这一差异。后来Lamb和Retherford通过实验确实测得 $2^{2} S_{1 / 2}$ 比 $2^{2} P_{1 / 2}$ 高出0.03 $c m^{- 1}$

实验装置

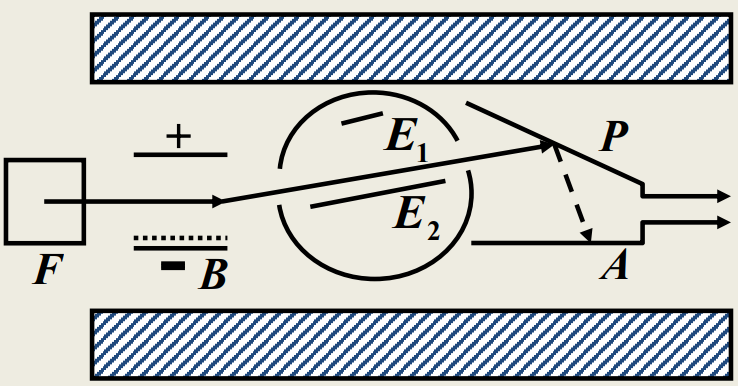
Pasted image 20240522043001.png|300 如图所示，氢气在F炉中分解为原子输出，在B区被电子撞击从而跃迁到激发态，调节B区的能量使得氢原子恰好被激发到n=2态( $2^{2} S_{1 / 2}, 2^{2} P_{1 / 2}, 2^{2} P_{3 / 2}$ ),这些原子运动到E区后，由于选择定则 $2 P$ 的氢原子自发跃迁到基态，而 $2^{2} S_{1 / 2}$ 态的原子作为亚稳态原子却无法直接跃迁回基态，这些原子撞击到钨板P上，激发态的原子将能量传给钨以跃迁回基态，而处于基态的氢原子仅仅只是碰撞到钨板上。而吸收到能量的钨的外层电子逸出达到阳极A，我们可以通过电流放大器测量PA间的电流强度，者可以反映亚稳态氢原子的数目。

如果，在E区增加一个电磁场，电磁波与亚稳态原子作用回使其跃迁到更高的激发态，随后使其跃迁回基态，这样能够处于亚稳态的原子大幅减少，PA间的电流应该降低。

实验时观察PA之间的电流，当电流发生锐减时表示电磁波频率符合能极差要求。

在Lamb和Retherford实验时发现若 $2^{2} S_{1 / 2}$ 与 $2^{2} P_{1 / 2}$ 能量相同则需要吸收频率为10950MHz的电磁波，但是实际上吸收值比预测值低了1000MHz，这恰好对应了0.03 $c m^{- 1}$ 的波数，这种 $2^{2} S_{1 / 2}$ 比 $2^{2} P_{1 / 2}$ 高出0.03 $c m^{- 1}$ 的现象称为Lamb位移，这一发现直接推动了量子电动力学的诞生！！！

Lamb位移

对具有相同 n,j 的两能级而言，若 l 不同，其能级也不相同. 各个 $^{2} S_{1 / 2}$ 能级比 $^{2} P_{1 / 2}$ 能级高.
同时对于同一个n值，j= $\frac{1}{2}$ 时Lamb位移最大， $j > \frac{1}{2}$ 的能级的Lamb位移几乎可忽略。
n越大，Lamb位移越小。（能级差与 $\frac{1}{n^{2}}$ 成正比，因此Lamb位移也越来越小）

电子的反常磁矩

$g_{s} = 2 (1 + a)$ 首先由库什和弗利在实验中发现。 a表示g因子与2的差别，称为电子的反常磁矩.^[1]

然而狄拉克的相对论量子力学无法对其进行解释，后来发展出的QED，即量子电动力学对其做出了一定的解释（理论计算值实验值之间十分的精确。） ↩︎