Bohr's H Atom model(old quantum)
黑体辐射
早在18世纪人们就发现物体在高温下会发出光,通常是红色的。由于卢瑟福的“核式”原子模型对原子光谱等问题无法解释,因此一个新的理论被迫切的需要。
- 热辐射
- 黑体
- 平衡热辐射
- 基尔霍夫辐射定律:
- 定义:光谱辐出度(单位面积的辐射功率)
——单位时间内,从物体单位表面发出的在频率 附近单位频率间隔内的电磁波的能量,即 ,其中 为辐射场能流密度。同时 。但是基尔霍夫并未给出辐射能流密度的具体表示。
- 定义:光谱辐出度(单位面积的辐射功率)
- 维恩公式:
- 1896年维恩分析实验数据,通过热力学理论获得:
, 为常量,该公式只在温度较低是与实验数据较为吻合。 - 维恩位移公式:
,该公式可以从韦恩公式求极值得到;常被用来估计恒星温度。
- 1896年维恩分析实验数据,通过热力学理论获得:
- 斯特藩-玻尔兹曼定律
- 一个发热物体单位面积的总功率与其温度的关系。
- 辐射通量()
, .
- 瑞丽-金斯公式
- 瑞利认为,黑体空腔中的电磁波 在腔的内壁不断地反射,只有以驻波的形式存在,才能使其不因叠加而湮灭。
- Planck 公式
- Planck 公式是由其本人拼凑出来的,以下是现代解释和相关的推导。
- 费米子和玻色子分别遵循费米-狄拉克分布和玻色-爱因斯坦分布
; .而当能级简并度极大时两者均趋于麦克斯韦-玻尔兹曼分布: . - 光子作为玻色子,达到平衡后服从玻色-爱因斯坦分布。黑体内部空腔中不断吸收和发射光子,光子气体中的光子数是不守恒的,只有能量守恒的限制。
- 在量子力学中,边长为L的容器中的自由粒子动量分量的可能的值为:
,其中 . n为对应量子态的粒子数.当L很大时作准连续处理: . - 则动量在
范围内的粒子的量子态数 为:
换成球坐标对方向角积分,并代入德布罗意关系和偏振自由度2得到
则在
每个光子能量为
亦即:
- 维恩公式和瑞丽-金斯公式以及斯特潘-玻尔兹曼定律均可由普朗克公式导出。

光电效应
1887年,海因希里·赫兹[1]在用真空阴极射线管做实验时偶然发现了紫外线照射下阴极射线管中产生了光电流。光电效应就此发现。
随后JJ·汤姆孙的研究还发现改变入射光的波长和强度,电流会分别发生不同的变化。
- 光电子的动能(光电流是否产生)仅与入射光的频率有关。
- 改变光照强度可以改变电流的大小。
实验装置:
········································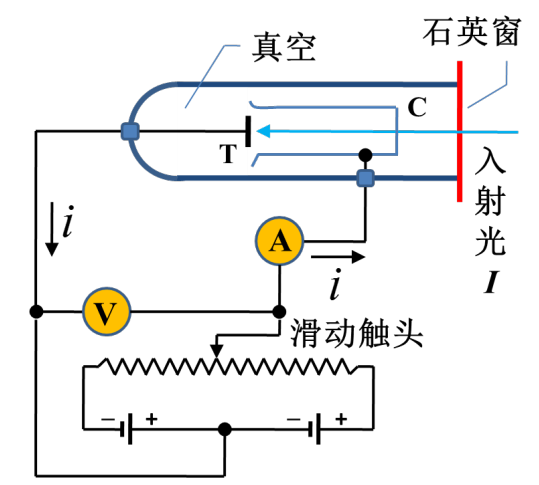
通过改变电压的的大小和入射光的频率以及强度来进行研究:
- #遏止电压
- U=0 甚至U<0时,即电场阻止电子飞翔阳极,但仍有电子可以达到阳极,直到反向电压达到一定大小后,电流才消失。
- 遏止电压与入射光频率成正比。
- 即
- #饱和电流
- 从零开始增加正向电压,光电流逐步增大,直到某一电压大小后,光电流不在变大。
- 达到饱和电流后,增大光强,则此时电流不再饱和。
- 在电压和入射光的频率固定时,单位时间内,释放的光电子数与入射光强正比。
- #截止频率
- 对某一金属材料,入射光的频率要达到某一个特定的频率才能产生光电流,在此之前,无论光强多大都无济于事[2]。
- 这个频率下限被称为截止频率(红限)。
- 不同的(金属)材料的红限不同。
- #瞬时性
- 光电效应的不需要时间积累,也不能时间积累。
- 现代研究结果表明:
.
至此,光的波动说遇到了困难,其结论与上述实验现象相悖。
爱因斯坦在1905年提出了光子假设,认为光的能量是量子化的。光量子与电子作用将自身能量全部交给电子,使电子得到大于逸出所需的能量从而逸出。从而:
W是逸出所需的能量,称为逸出功。
密里根通过
1916年爱因斯坦将光量子的概念进行延拓(来自狭义相对论),提出光量子具有线动量并满足:
光电效应的应用:光电倍增管,红外夜视仪。
氢原子光谱
起初,没人将原子光谱和基础物理联系起来,因为前者看起来似乎过于复杂。
1885年,巴尔末对氢原子光谱进行总结,提出了经验公式:巴尔末公式
光谱上与该公式吻合的谱线被称为,巴尔末线系。
此后不同的科学家分别又找出了:
- Lyman系
- Balmer系
- Paschen系
- Brackett系
- Pfund系
在1889年,里德伯根据经验规律总结出了经验公式:
该公式很好的描述了氢原子的光谱谱线,却没有合适的理论解释。
1913年2月,Bohr注意到了巴尔末公式并得到了灵感,提出了新的原子构型理论。
首先,Bohr提出了三条假设:
- 定态假设:氢原子电子只能在一系列分立的轨道上绕核运动,且无电磁辐射,即原子由一系列定态。
- 跃迁假设:假设原子内部能量守恒,电子要改变轨道必须从外界获得能量。根据光电效应,电子通过吸收一定频率光子进行跃迁。
. - 电子轨道角动量量子化假设:
即电子轨道角动量必须满足上式[3]。
#对应原理: 微观范围内与宏观范围内的现 象遵循各自的规律;但将微观范围内的规律 延伸到经典范围时,所得结果应与经典规律 所得到的相一致。
根据对应原理:由频率法则和对应原理
在将其与电子得静电势能联立:
当n很大时,考虑相邻轨道之间的跃迁:
此频率应与电子轨道频率一致:
公式(1),(2)两式应一致,由此导出里德伯常量
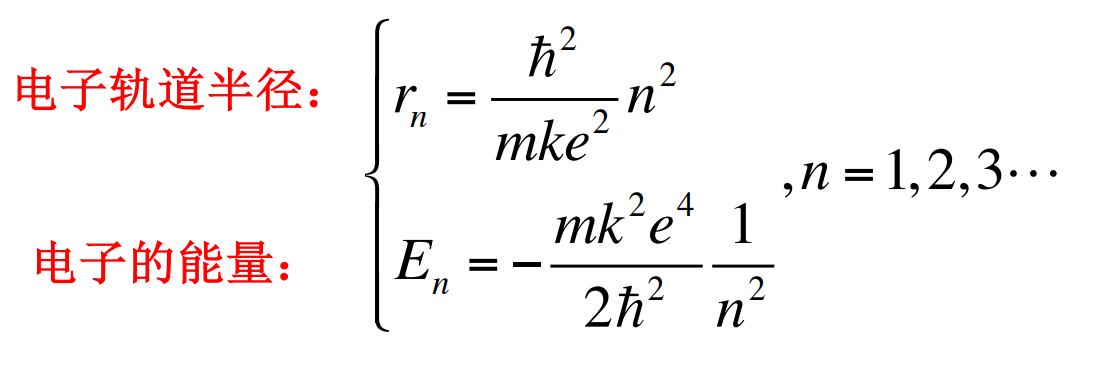
可见轨道和能量都是量子化的。
再由:
代入角动量公式:
再代入
这就是Bohr得角动量量子化假设条件。
第一Bohr半径:
精细结构常数:
精细结构常数的推导:
由此还可以得:H原子的第一电离能为13.6eV
#电子的速度
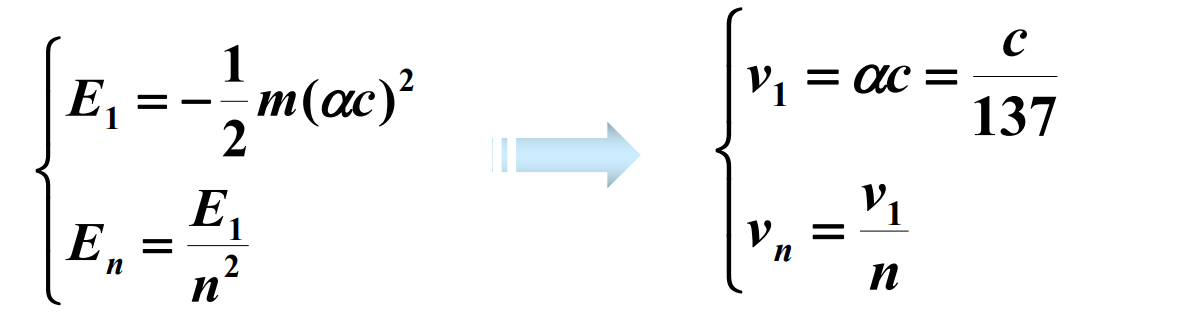
当实验的精度提高后,里德伯常量的实验值与理论值出现了约0.05%的偏差
Bohr提出,该偏差是由之前假设原子核静止不动造成的,尽管H核与电子的质量差别有1800倍,H核仍会因受到库仑力而存在一个圆周运动。
于是将约合质量代替原来公式中的电子质量:
Bohr理论的实验验证
夫兰克-赫兹实验
- 微观粒子弹性碰撞的定义
- 弹性碰撞:当两粒子碰撞时,只有粒子动能的交换,内能不变。 产生条件: 碰撞粒子动能较小
- 非弹性碰撞:当两粒子碰撞时,粒子内部的能量有变化。
- 将阴极射线管装置改装,向内充入汞蒸气,调节入射电子加速电压使其达到不同动能。若某一动能状态下的电子达到另一极板的数量突然减少,说明电子的动能被吸收。
- 根据Bohr的理论,Hg原子的第一激发态到基态的能量为4.9eV,则若入射电子在动能为4.9eV时与Hg的电子发生非弹性碰撞,产生能量交换,则上述的电流在加速电压为4.9V时应该存在一个吸收峰。
- 实验结果如图:
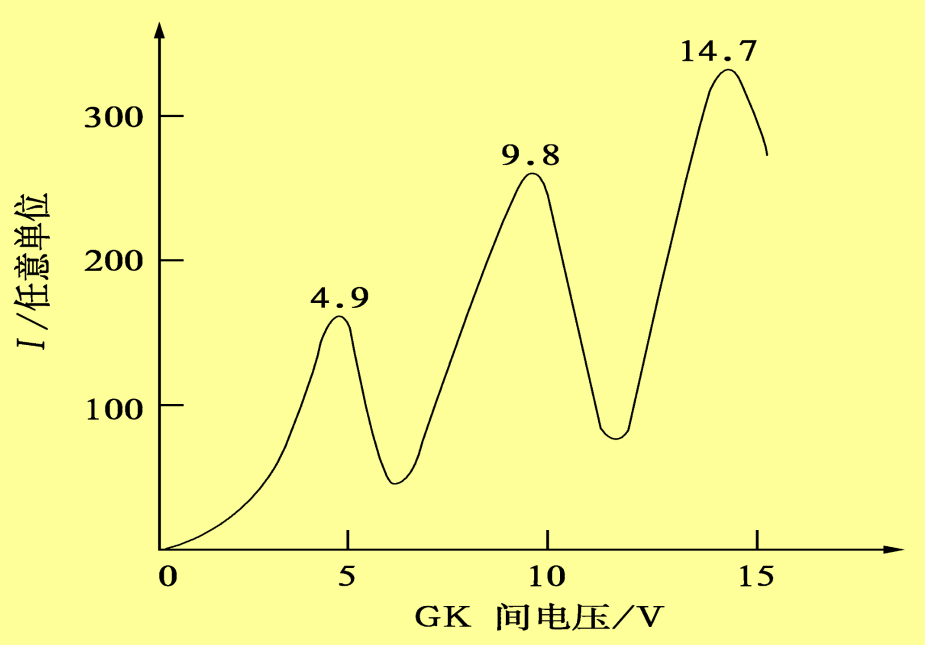
说明了假设初步成立。 - 实验的改进: 将电子的加速区与汞蒸气分开,这样可以使电子满足Hg原子不同能级差大小的动能。
Bohr理论的延申
类氢原子光谱
#He原子光谱--毕克林线系
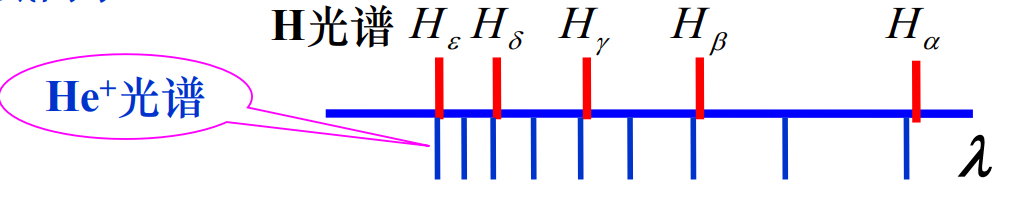
Bohr为此给出了对里德伯常量R的修正:即在原公式中出现
氢的同位素的发现
1932年,美国物理化学家尤雷发现
里德伯原子
将多电子原子的最外层的一个电子激发到n很大的轨道上,可以认为内层电子的屏蔽效应使之成为了一个巨大的,带正电荷为1的原子。因此也可将其看为类氢原子,能够用Bohr的理论描述。
里德伯原子的半径很大,有的甚至接近细菌的大小,其寿命更是接近千分之一秒。
奇特原子
由
于μ子的质量是电子质量的200多倍,因而奇特原子的半 径比普通原子小很多。
电子偶素
正负电子形成的电子偶素也可用Bohr的理论来描述。(两个电子的质量都不能忽略)
Bohr—索墨菲模型
早在1896年,迈克尔逊和莫雷就发现了氢原子光谱存在更精细的结构,为了解释该现象,索墨菲将Bohr的理论做出了两点推广:
- 椭圆轨道假设:
- 索墨菲认为,对于n能级处的电子有n个偏心率不同的简并轨道,这可以解释部分的精细结构和元素周期律(目前科学界认为这个理论是错误的。)
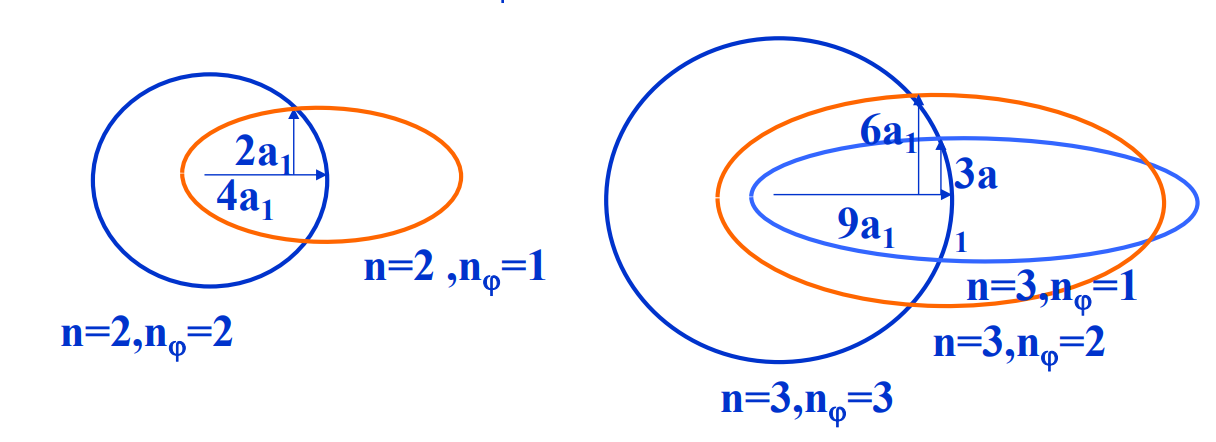
- 索墨菲认为,对于n能级处的电子有n个偏心率不同的简并轨道,这可以解释部分的精细结构和元素周期律(目前科学界认为这个理论是错误的。)
- 相对论效应:
- 按照相对论原理,物体的质量随他的运动速度而改变:
物体动能:
对于圆轨道:
现代理论一般认为这个是正确的。
Bohr理论的成功之处:
- 从理论上圆满地解释了氢光谱的经验规律 “里德伯公式”
- 用已知的物理量计算出里德伯常数,而且和实验值符合得较好。
- 较成功地给出了氢原子半径的数据。
- 定量地给出了氢原子的电离能。
不足之处困难